Quantum Fluid Dynamics

Many-body quantum dynamics hinges on the quantum statistics of the particles. Identical bosons tend to occupy the same quantum state, leading to large scale quantum phenomena with sometimes classical features. Emergent collective behavior in many body quantum systems leads naturally to exploring the the quantum nature of fluids: what is a quantum fluid? What aspects of quantum fluid dynamics are uniquely quantum in origin, and what is instead universal to much wider class fluids?

Vortices

Since their discovery, quantum vortices have provided key evidence for superfluidity. Onsager saw that the existence of a superfluid order parameter \(\psi=\sqrt{\rho}e^{i\theta}\) constrains quantum vortices in a BEC to integer circulation, \(n\), around any simply connected closed contour. The velocity originates from the quantum quantum phase \(\mathbf{v}=\hbar \nabla \theta/m\), and so the circulation is quantized:

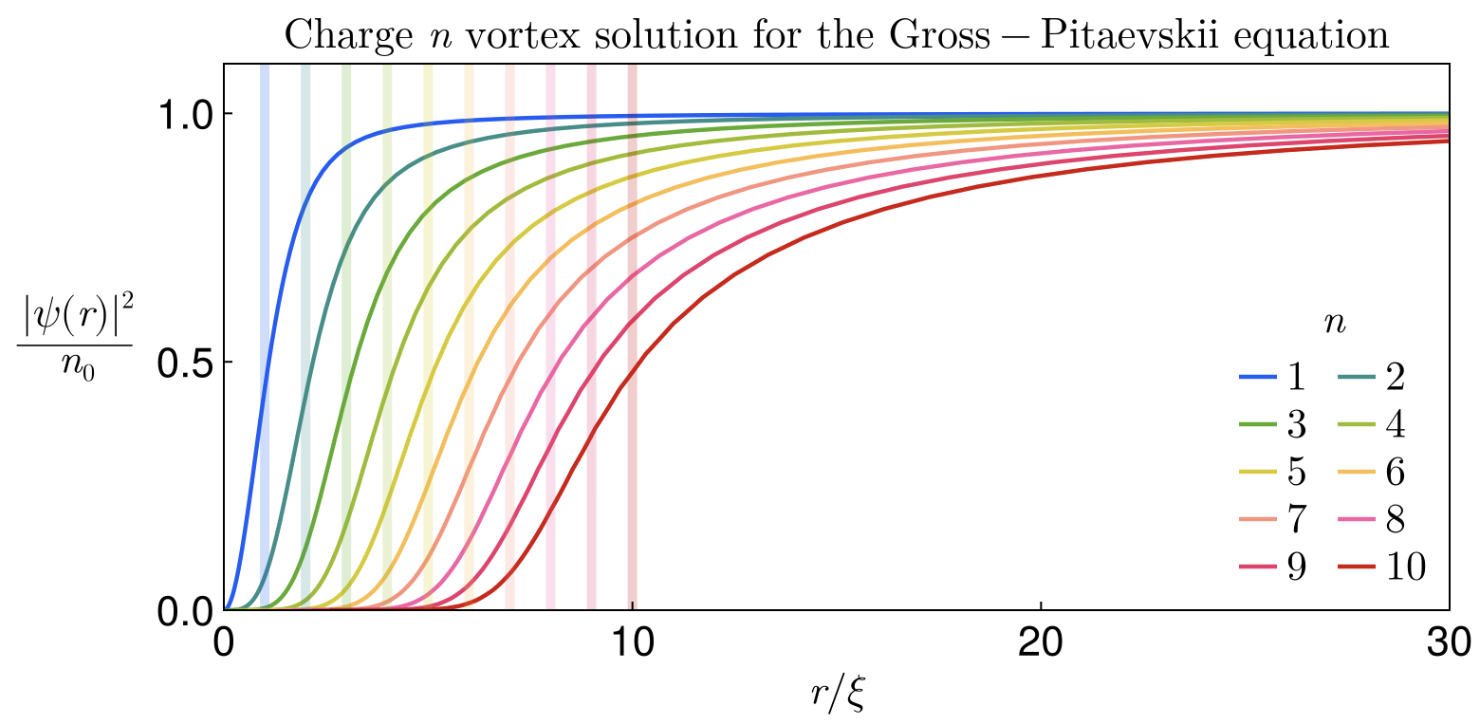
\[\oint \mathbf{v}\cdot d\mathbf{l}=n\frac{h}{m}.\]

Creation and destruction of vortices is thus subject to topological constraints that do not hold for classical fluids. Charge \(n\) solutions of the Gross-Pitaevskii equation have radius of \(\sim n\xi\) where \(\xi=\hbar/mc\) is the Compton wavelength for energy \(\mu\) the chemical potential. However, only \(n=1\) is thermodynamically and dynamically stable and therefore seen in experiments.

Quantum Turbulence

Quantum fluid dynamics can support classical wave motion, and uniquely quantum dynamics associated with vortices.

In quantum turbulence the intrinsic quantum properties of the fluid are central to the transport of energy in a turbulent cascade. Classical fluid phenomena such as Kolmogorov turbulence with associated \(k^{-5/3}\) energy spectrum have been subject to intense study in quantum fluids, and are a very active area of experimental investigation.

In 2013, in collaboration with Brian Anderson at U Arizona, my group theoretically demonstrated the possibility of a Kraichnan inverse-energy cascade in two-dimensional quantum turbulence. We also proposed avenues to create large scale vortex clustering with negative Boltzmann temperature of vortices. Our collaboration with Tyler Neely’s group at University of Queensland led to the first observations of negative temperature quantum vortices, confirming Onsager’s 1949 prediction.

Spectral Analysis

Compressible quantum fluids such as BEC or QFL support quantum vortices, compressible phonon excitations, and quantum pressure. Understanding energy transport in scale space requires correctly accounting for the quantum phase in each of these features of the fluid.

We are developing new techniques for spectral analysis of compressible quantum fluids to gain deeper insight into the nature of quantum turbulence.

Associated publications